Pre- relativistic physics

  The starting point for our work are Newtons laws  of motion. These can be stated as follows:

• Free particles move with constant velocity.
• The vector force is proportional to the rate of change of momentum i.e. .
• To every action there is an equal and opposite reaction.

The first of these laws singles out inertial frames  as the non- accelerating ones.

Consider now a frame [ i.e. a set of spatial coordinates (x,y,z) and a time coordinate t ], and another frame with coordinates which moves in the x direction with uniform speed v relative to the frame .

Common sense suggests that the two sets of coordinates are related by

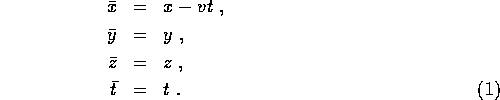
These are the Galelian transformations  .

 

Figure 1.1: I do not know what I may appear to the world; but to myself I seem to have been only like a boy playing on the sea- shore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me. Isaac Newton.

If the particle has a velocity with components in , its velocity in is:

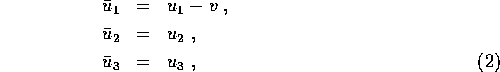
or

where

More generally if the coordinate axes and the origins of and differ then:

where has components (x,y,z). Here is a rotation matrix aligning and , is the relative velocity of with respect to and is the displacement of the origin from .

Since the transformation is linear [ constant velocity in constant velocity in ], is inertial if is.

Thus there are an infinite set of inertial frames, all moving uniformly with respect to each other.

All of Newtons laws apply in any inertial frame since

and is invariant. Thus we have Newtonian [ Galelian ] Relativity.

The laws of mechanics do not allow measurement of absolute velocity, however one can measure absolute acceleration.

Newton explained inertial frames in terms of absolute space  identified with the center of mass of the solar system or a frame of ``fixed stars''. However this is unsatisfactory because:

• There is no unique identification [ many inertial frames ].
• Philosophically unappealing since absolute space affects everything but is affected by nothing.